Differential equations and linear algebra form the foundation of modern problem-solving in STEM fields․ They model complex phenomena and provide tools for analyzing systems, enabling precise solutions in physics, engineering, and more․
What Are Differential Equations?
Differential equations are mathematical equations that relate a function to its derivatives․ They describe how quantities change over variables like time or space․ These equations are fundamental in modeling real-world phenomena, such as population growth, heat transfer, and fluid dynamics․ Differential equations can be classified into types: ordinary (involving one variable) and partial (involving multiple variables)․ They are also categorized by order, which refers to the highest derivative present, and degree, the highest power of the derivative․ Linear differential equations, where the function and its derivatives are linear, are widely studied due to their solvable nature․ Nonlinear equations, while more complex, often describe intricate systems․ Solving these equations provides insights into the behavior of physical, biological, and economic systems, making them indispensable tools in scientific analysis and engineering applications․
Role of Linear Algebra in Solving Differential Equations
Linear algebra plays a pivotal role in solving differential equations by providing essential tools and frameworks․ Key concepts such as vector spaces, matrices, and linear transformations enable the analysis of complex systems․ For instance, systems of linear differential equations can be expressed in matrix form, simplifying their solution using techniques like eigenvalue decomposition․ Linear algebra also underpins methods for solving systems of equations, which often arise in discretized forms of differential equations․ Additionally, the concept of linear independence is crucial for constructing fundamental sets of solutions․ By leveraging matrix operations and properties, such as determinants and inverses, linear algebra offers systematic approaches to handle both homogeneous and non-homogeneous equations․ This interplay between linear algebra and differential equations is fundamental in fields like physics and engineering, where these mathematical tools are indispensable for modeling and solving real-world problems․
Key Concepts in Linear Algebra for Differential Equations
Vector spaces, linear transformations, and matrices are foundational․ Eigenvalues and eigenvectors aid in solving systems, while determinants and inverses simplify equation handling․
Vector Spaces and Linear Transformations
Vector spaces provide a framework for understanding linear structures, while linear transformations describe mappings between these spaces, preserving their algebraic properties․ In the context of differential equations, these concepts are essential for analyzing systems of equations and simplifying complex problems․ Vector spaces allow the representation of solutions to differential equations as elements within a structured environment, enabling the use of powerful algebraic tools․ Linear transformations, on the other hand, facilitate the study of how these solutions evolve under various operations․ Together, these ideas form the backbone of modern approaches to solving differential equations, offering a systematic way to handle both homogeneous and non-homogeneous systems․ By leveraging vector spaces and linear transformations, mathematicians and engineers can uncover underlying patterns and predict the behavior of dynamic systems with greater precision․
Matrices and Systems of Linear Equations
Matrices and systems of linear equations are fundamental tools in both linear algebra and differential equations․ A matrix is a rectangular array of numbers, symbols, or expressions, while a system of linear equations involves equations where variables and their coefficients are arranged in a linear fashion․ These concepts are crucial for solving complex problems, as they provide a structured way to represent and manipulate data․ In the context of differential equations, matrices are often used to represent systems of equations, enabling the application of powerful solution techniques․ For example, systems of linear differential equations can be expressed in matrix form, simplifying the process of finding solutions․ Additionally, matrices play a key role in numerical methods for solving differential equations, such as finite difference methods․ Understanding matrices and systems of linear equations is essential for advancing in both fields and applying these concepts to real-world problems in physics, engineering, and beyond․
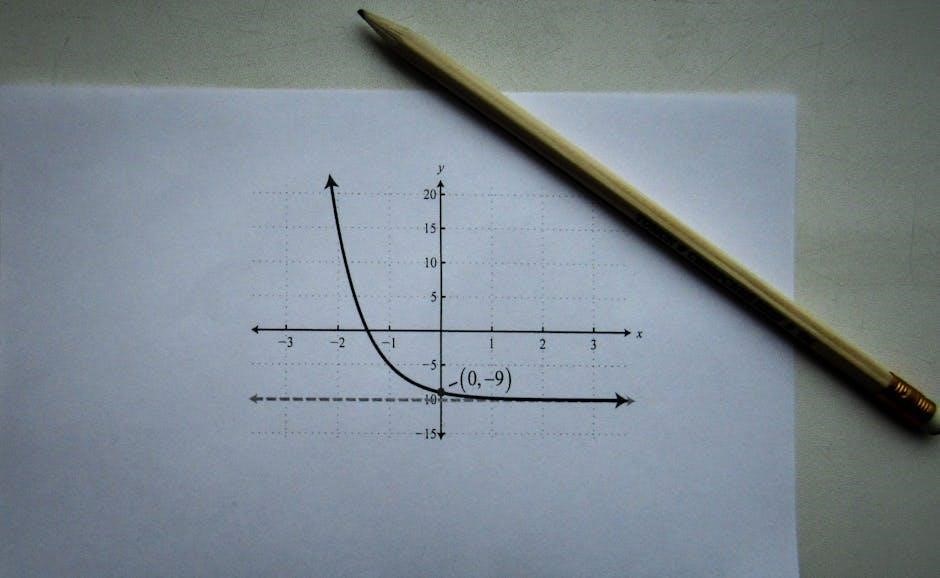
First-Order Differential Equations
First-order differential equations involve functions and their first derivatives․ They are fundamental in modeling various phenomena, such as growth rates and mixing problems․ Key methods include separable and exact equations․
Separable Equations and Exact Equations
Separable equations are a subclass of first-order differential equations where variables can be isolated on different sides of the equation․ This allows integration to find the solution directly, making them relatively straightforward to solve․ Exact equations, however, involve a differential form that satisfies the condition of exactness, meaning the equation can be derived from a potential function․ Solving exact equations often requires identifying an integrating factor to make the equation exact if it isn’t already․ Both methods are essential tools in solving first-order differential equations and are widely used in modeling real-world phenomena, such as population growth, mixing problems, and electrical circuits․ These techniques are introduced in courses and textbooks, such as those by Paul Dawkins and Boyce & DiPrima, to provide foundational problem-solving skills in differential equations․
Higher-Order Linear Differential Equations
Higher-order linear differential equations involve derivatives of a function beyond the first order․ They are solvable using methods like characteristic equations and are crucial in modeling mechanical vibrations and electrical circuits․
Characteristic Equations and Homogeneous Solutions
Characteristic equations are fundamental in solving higher-order linear differential equations․ By assuming a solution of the form ( e^{rt} ), these equations help determine the roots ( r ) that define the structure of the homogeneous solution․ Real, distinct roots yield exponential functions, while repeated or complex roots introduce polynomial and trigonometric components․ These solutions form a fundamental set, enabling the construction of the general solution through linear combinations․ Understanding characteristic equations is essential for addressing both homogeneous and non-homogeneous cases, providing a systematic approach to solving various physical and engineering problems․ This method bridges differential equations with linear algebra, emphasizing the role of eigenvalues and eigenvectors in dynamic systems․ Mastery of characteristic equations is crucial for advancing in applied mathematics and its applications․

Applications of Differential Equations in Physics and Engineering
Differential equations model real-world phenomena like mechanical vibrations, heat transfer, fluid dynamics, and electric circuits․ They are essential for analyzing and designing systems in physics and engineering applications․
Modeling Real-World Phenomena with Differential Equations
Differential equations are powerful tools for modeling dynamic systems and understanding complex phenomena in physics, engineering, and other sciences․ They describe how systems change over time or space, enabling precise predictions and analyses․ From population growth to fluid dynamics, these equations capture the essence of real-world processes․ In physics, they model oscillations, heat transfer, and wave propagation, while in engineering, they are used to design structures, optimize systems, and understand signal processing․ Biological systems, such as disease spread or cellular behavior, also rely on differential equations for accurate modeling․ By translating physical laws into mathematical expressions, these equations provide a framework for solving practical problems and simulating scenarios, making them indispensable in scientific and technological advancements․
Resources for Learning Differential Equations and Linear Algebra
Extensive PDF notes and textbooks are available online, offering detailed insights into differential equations and linear algebra․ These resources cover fundamental concepts, practical examples, and advanced problem-solving techniques for students and professionals․
Recommended PDF Notes and Textbooks
For comprehensive learning, several high-quality PDF notes and textbooks are available․ Paul Dawkins’ Differential Equations Notes from Lamar University provide detailed explanations of key topics like separable equations, exact equations, and systems of differential equations․ Additionally, Simon J․A․ Malham’s Lecture Notes from Heriot-Watt University offer insights into linear differential equations and their applications․ Marshall Hampton’s online book from the University of Minnesota Duluth covers first-order ODEs, applications, and numerical methods․ These resources are widely used and respected in academia․ They include exercises, solutions, and real-world examples, making them invaluable for both students and professionals․ PDF versions ensure accessibility and convenience for self-study or classroom use․ These materials are regularly updated and align with modern teaching standards, ensuring a robust understanding of both differential equations and linear algebra․
